3DCS
Product Description
鑫威資訊股份有限公司
RSS與蒙地卡羅法公差分析比較
物體在空間中有六個自由度，一維公差分析只能考量單一自由度，而三維公差分析可以考量六個自由度，更多自由度能有更精確的分析結果、考量更多的變異(例如旋轉、偏擺、多方向變異)、更符合產品實際需求。
以下為一維公差分析常碰到的問題:
- 一維公差皆假設為線性，如果是幾何公差無法呈現。
- 一維公差分析一次計算只能看單一目標，如果觀測目標多則曠日廢時。
- 一維公差分析無法視覺化呈現變異，只能從數值想像組裝後情形。
- 分析只能單維分析，無法同時考量多維度，如角度量測、軸孔Floating皆無法分析。
- 一維分析將公差皆假設維常態分佈，實際上產品不一定是常態分佈。例如鑽孔會因為鑽頭磨耗，尺寸會是偏小的情形。
- 無法計算各公差影響比重，改善品質不易。
- 無法考量製程因素，只能進行公差的數值計算。
以上問題使用3DCS皆可以解決。
我們使用兩個模型呈現一維公差分析與三維公差分析的差別。
一維公差分析與三維公差分析堆疊組立結果差異
三個方塊平面度為2，請問三個方塊堆疊組裝後高度分佈是多少?
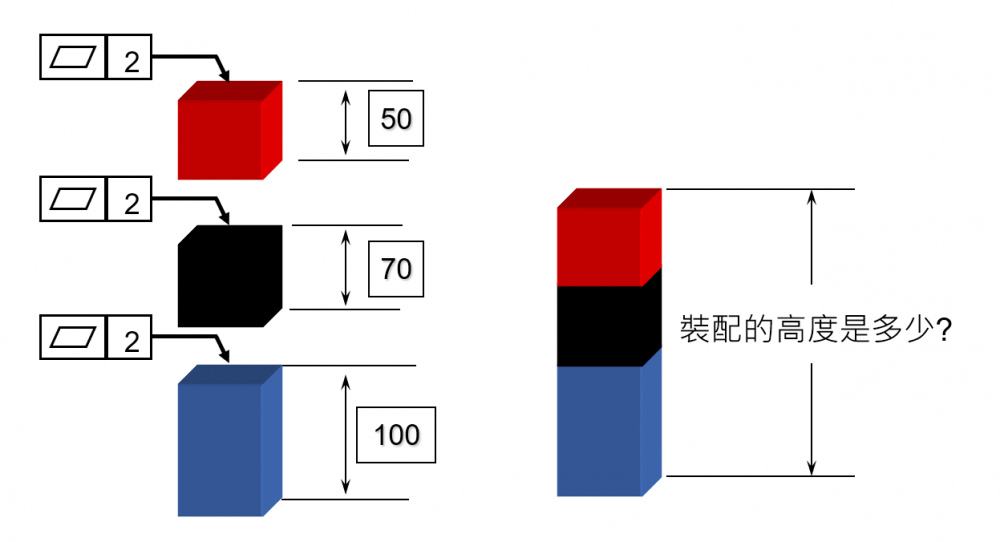
平面度是一個多維度變異，透畫以下動畫可以了解如果採用RSS無法呈現平面度造成的偏擺。
使用3DCS可以精確的模擬平面度造成的偏擺變異。
三方塊裝配後量測高度
| 一維分析結果 | 三維分析結果 |
| 使用Excel計算 結果為3.46mm
|
使用3DCS計算 六標準差結果為2.28mm。
|
結論：RSS方法比3DCS結果多出34%，代表使用一維公差分析會得到過於嚴苛的結果，導致公差要更小成本更高。
軸孔定位案例說明
兩軸孔定位，軸孔大小公差皆為±1mm與正位度1。觀測目標為5mm的間隙，分別量測上中下三個位置。
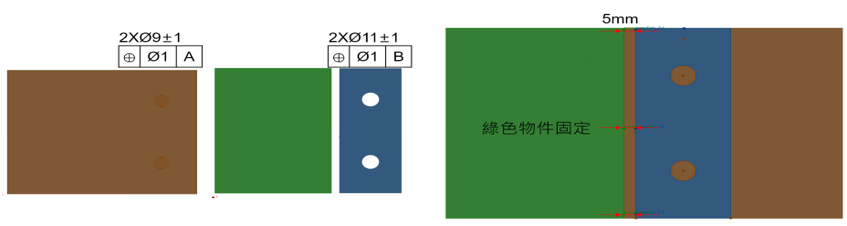
下圖呈現三維分析中軸孔裝配產生的Floating偏擺效應，而一維公差分析只能呈現單一方向。
三維分析更符合實際組裝獲得更精確的結果。
計算結果
| 一維分析結果 | 三維分析結果 |
|
使用Excel計算
|
使用3DCS計算 三維分析考量多維度變異，因軸孔Floating會導致上下量測點偏擺較大、而中間量測點偏擺較小。 在3DCS計算結果，上下量測點六標準差大約為5.67中間量測點六標準差大約2.46。
|
在範例中，一維公差分析會過度簡化問題沒有考量軸孔Floating效應。
上下量測點Excel結果比3DCS結果少了44%
中間量測點Excel結果比3DCS結果多出28%
結論
一維公差分析只考量單一方向、公差假設為常態分佈、無法考量製程變異等種種原因，導致計算結果與實際結果產生落差。
三維公差分析呈現全面的變異、考量非常態分佈、考量製程變異、視覺化呈現組裝變異、考量幾何因子(GeoFactor)獲得更符合實際情形的分析結果。