3DCS
Product Description
3DCS模組介紹
3DCS為了使更多情境都能獲得更精確的結果，不只能提供一般靜態分析外，還提供了另外 三個模組，能分析動態做動件、物件受力變形、分析後自動優化，分別為動態分析模組(MMC) 、最佳化模組(AAO)、有限元分析模組(FEA)
3DCS動態分析模組
許多產品裝配後是動態運作的例如風扇、馬達、引擎、機械手臂等等。
3DCS 透過獨特且先進的手法來分析物件做動時的變異，確保物件在整個做動流程都是符合使用者的需求。
3DCS有限元分析模組
傳統的公差分析往往被零件視為”鋼體”，但實際上零件並非鋼體，
當物件受到重力、鎖固、焊接、溫度變化往往會使物件變形。
3DCS整合有限元素法(FEA)考量物件受到外力後造成變形，讓三維公差分析更精準符合實際情形。
3DCS最佳化模組
做完公差分析發現產品品質不佳卻不知從何開始改善公差?
做完公差分析確認產品品質沒問題，成本太高想放寬公差卻不知道從何放寬?
3DCS AAO(最佳化)模組同時考量製程花費和製程能力來進行公差的優化、達到降低成本、增加精度的結果。
3DCS公差分析產生效益
提高質量
- 3DCS提供可視化結果，確認組裝後品質。
- 3DCS提供詳細分析數據，提供明確方向改善品質。
減少設計變更
- 在3DCS中可以了解組裝後的問題，並立即在3DCS中進行設計變更。
減反重工以及報廢
- 在設計階段即可預測不良率以及問題，大幅減少修正和報廢的可能。
精準呈現真實變異
- 三維公差分析比起一維公差分析更能呈現實際情況，預測結果更精確。
- 結果數據豐富，更了解組裝結果以及改善方向。
3DCS支援多種CAD軟體
3DCS直接嵌入在CAD軟體中，支援CAD包括:SolidWorks、Creo、CATIA、NX、Inventor。
3DCS特別的是有獨立版本，不用開啟CAD軟體也能進行公差分析，具有輕便、更新快 速(不用於CAD軟體溝通)、穩定(不用配合CAD軟體)。
使用者可以依據個人需求選擇與CAD嵌入的版本或獨立版本。
設計時常發生公差已經很精密了但裝配後還是發生問題，問題往往不是在公差設計而是出現在裝配位置和裝配手法。
GeoFactor是3DCS中考慮幾何因素影響的一個模組，對零件和工裝的定位是如何影響整個組裝品質進行分析，使我們理解定位系統和組裝品質之間的關係。
3DCS Geofactor 用在設計階段評估零件幾何結構、組裝序列和組裝方法對產品的組裝品質的影響，以改進設計和製程的穩健性。
(三張圖形說明Geofactor，當Geofactor越大表示公差變異對量測目標影響越大。)
透過GeoFactor我們可以了解哪些公差的變異容易對量測目標造成影響，可以將該公差縮小或是更改組裝方法提高品質。
GeoFactor分析：對影響設計目標的幾何結構和定位系統進行分析。
- 係數反映了真正的公差效應。
- 反映了公差是如何被零件的幾何形狀放大。
- 關注設計的穩健性而不是公差。
- 為設計驗證提供數值結果。
無論一個公差範圍有多小，都能對整個組裝公差產生一個較大的影響，在設計中識別並解決這些影響，對於一個零組件來說，是非常重要的。
物體在空間中有六個自由度，一維公差分析只能考量單一自由度，而三維公差分析可以考量六個自由度，更多自由度能有更精確的分析結果
、考量更多的變異(例如旋轉、偏擺、多方向變異)、更符合產品實際需求。
以下為一維公差分析常碰到的問題:
- 一維公差皆假設為線性，如果是幾何公差無法呈現。
- 一維公差分析一次計算只能看單一目標，如果觀測目標多則曠日廢時。
- 一維公差分析無法視覺化呈現變異，只能從數值想像組裝後情形。
- 分析只能單維分析，無法同時考量多維度，如角度量測、軸孔Floating皆無法分析。
- 一維分析將公差皆假設維常態分佈，實際上產品不一定是常態分佈。例如鑽孔會因為鑽頭磨耗，尺寸會是偏小的情形。
- 無法計算各公差影響比重，改善品質不易。
- 無法考量製程因素，只能進行公差的數值計算。
以上問題使用3DCS皆可以解決。
我們使用兩個模型呈現一維公差分析與三維公差分析的差別。
一維公差分析與三維公差分析堆疊組立結果差異
三個方塊平面度為2，請問三個方塊堆疊組裝後高度分佈是多少?
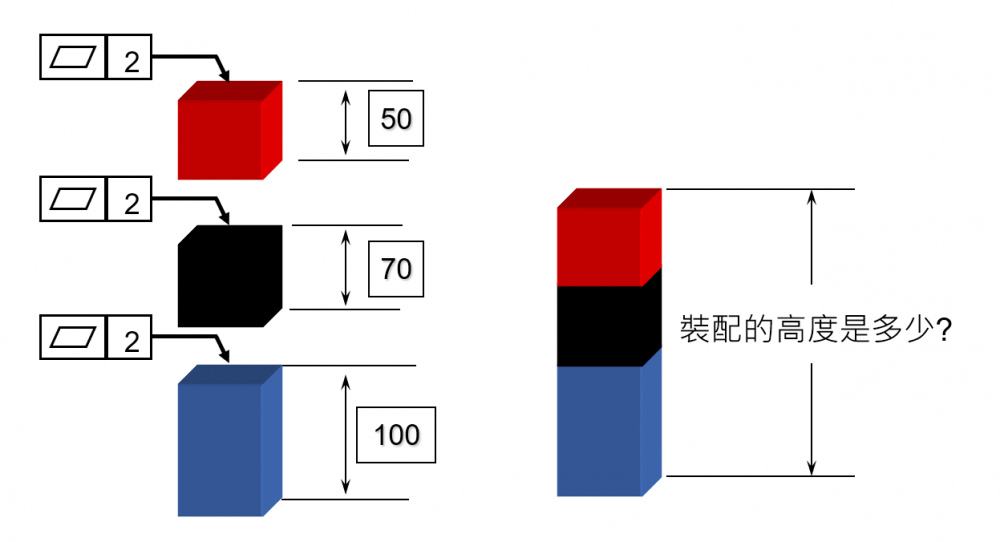
平面度是一個多維度變異，透畫以下動畫可以了解如果採用RSS無法呈現平面度造成的偏擺。
使用3DCS可以精確的模擬平面度造成的偏擺變異。
三方塊裝配後量測高度
| 一維分析結果 | 三維分析結果 |
| 使用Excel計算 結果為3.46mm
|
使用3DCS計算 六標準差結果為2.28mm。
|
結論：RSS方法比3DCS結果多出34%，代表使用一維公差分析會得到過於嚴苛的結果，導致公差要更小成本更高。
軸孔定位案例說明
兩軸孔定位，軸孔大小公差皆為±1mm與正位度1。觀測目標為5mm的間隙，分別量測上中下三個位置。
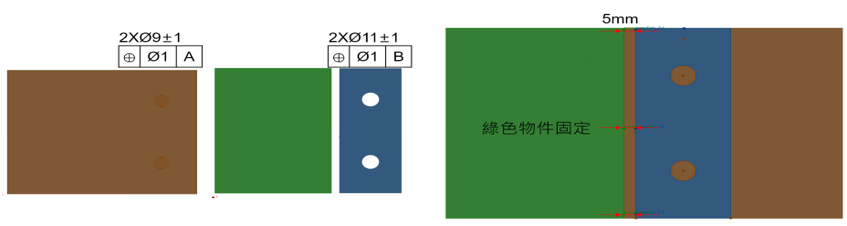
下圖呈現三維分析中軸孔裝配產生的Floating偏擺效應，而一維公差分析只能呈現單一方向。
三維分析更符合實際組裝獲得更精確的結果。
計算結果
| 一維分析結果 | 三維分析結果 |
|
使用Excel計算
|
使用3DCS計算 三維分析考量多維度變異，因軸孔Floating會導致上下量測點偏擺較大、而中間量測點偏擺較小。 在3DCS計算結果，上下量測點六標準差大約為5.67中間量測點六標準差大約2.46。
|
在範例中，一維公差分析會過度簡化問題沒有考量軸孔Floating效應。
上下量測點Excel結果比3DCS結果少了44%
中間量測點Excel結果比3DCS結果多出28%
結論
一維公差分析只考量單一方向、公差假設為常態分佈、無法考量製程變異等種種原因，導致計算結果與實際結果產生落差。
三維公差分析呈現全面的變異、考量非常態分佈、考量製程變異、視覺化呈現組裝變異、考量幾何因子(GeoFactor)獲得更符合實際情形的分析結果。
Worst case是傳統一維公差分析方法，計算方法是將公差值假設為最大或最小值，
再把全部公差進行累加，目的是為了確保無論公差如何變化都可以有100%的良率。
不過，使用Worst case方法常碰到以下問題：
- 一維公差分析只考量單一方向，無法考量偏擺、角度、旋轉，因此一維的Worst case並不是真正的最差狀況。
- Worst case因為要確保100%良率所以需要更精密的公差，導致成本提高。
- Worst case不是使用”統計”方法，只能判定組裝後是否在規格內而無法預測組裝後的分佈。
- 在實際組裝中Worst case不易出現，所有公差要同時出現在極端值的機率微乎其微，可能生產數百萬件才出現一件。
產品生產數量越多，越容易出現Worst Case
最差組裝在統計上會隨著生產數量越多出現機率越高，
因此生產一百萬件產品絕對比生產一萬件更容易出現糟糕的組裝結果。
這也說明了，我們必須透過統計手法才能準確考量Worst Case。
3DCS採用蒙地卡羅方法（又稱統計模擬法），能夠根據生產零件的數量產生不同的組裝結果，而這也更符合實際製程與產品組立後的狀態。
使用方塊堆疊說明組裝數量與Worst Case關係
三方塊平面度2進行堆疊組裝，公差最大時堆疊後高度為223mm、公差最小時堆疊後高度為217mm，最大最小最範圍為6mm。
使用3DCS進行計算，會發現隨著模擬組裝次數越多，最大最小範圍會越來越大。
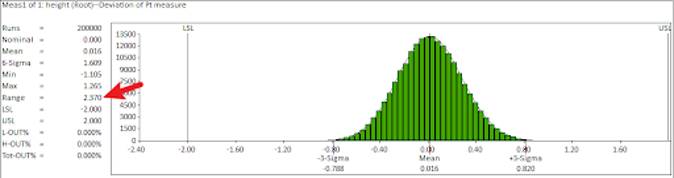
(如上圖，模擬組裝20萬次的最大最小範圍為2.37mm，遠小於預期的6mm。)
使用3DCS計算真正的Worst Case
對使用者來說除了軟體功能外，使用者介面是否友善也是關注重點
支援絕大部分的CAD格式包含:
系統需求
軟體運行穩定性較高並且消耗的電腦資源也比較低